|
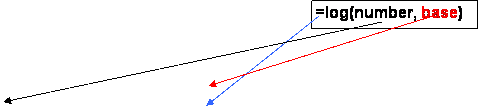
Other bases for logs. |
|
|
|
|
|
|
|
|
|
| ROW/COL |
B |
C |
D |
E |
F |
G |
H |
I |
|
| 4 |
|
| 5 |
|
| 6 |
There is nothing magic
about base 10 (or common logarithms). You could build logs on any base you
want. |
| 7 |
In
fact the log function has an option to set the base to any you may want to
use. |
|
| 8 |
|
| 9 |
Number |
log to the base 2 of the
number |
|
| 10 |
2 |
1 |
=2 ^ 1 |
|
| 11 |
4 |
2 |
=2 ^ 2 |
|
| 12 |
8 |
3 |
=2 ^ 3 |
|
| 13 |
16 |
4 |
=2 ^ 4 |
|
| 14 |
|
5 |
=2 ^ 5 |
|
| 15 |
64 |
6 |
=2 ^ 6 |
|
| 16 |
|
|
|
| 17 |
Other bases |
|
|
|
| 18 |
|
Base |
|
|
| 19 |
Number |
2 |
5 |
10 |
16 |
|
|
| 20 |
2 |
1.0000 |
0.4307 |
0.3010 |
0.2500 |
<=LOG($B20,F$19) |
|
|
| 21 |
4 |
2.0000 |
0.8614 |
0.6021 |
0.5000 |
|
|
| 22 |
5 |
2.3219 |
1.0000 |
0.6990 |
0.5805 |
|
|
| 23 |
10 |
3.3219 |
1.4307 |
1.0000 |
0.8305 |
|
|
| 24 |
16 |
4.0000 |
1.7227 |
1.2041 |
1.0000 |
|
|
| 25 |
20 |
|
1.8614 |
1.3010 |
1.0805 |
|
|
| 26 |
|
=LOG($B25,C$19) |
|
|
| 27 |
The blue numbers are the
logs of the number for different bases |
|
|
| 28 |
Notice that when the base
is equal to the number the log is always 1 |
|
| 29 |
|
| 30 |
Natural logarithms |
|
| 31 |
|
| 32 |
Look at the following
expansion: |
|
| 33 |
X |
(1+1/X)^X |
As
X expands the value of expression increases, but at a slower and slower rate
and reaches a limit. This limit is a number which like pi, never rounds off
even. This number is called "e." It has a lot of useful
mathematical properties. Because of this it is used frequently. As an example
the derivative of e^x is e^x. Very convenient. |
|
| 34 |
1 |
2.00000 |
|
| 35 |
2 |
2.25000 |
|
| 36 |
3 |
2.37037 |
|
| 37 |
4 |
2.44141 |
|
| 38 |
5 |
2.48832 |
|
| 39 |
6 |
2.52163 |
|
| 40 |
7 |
2.54650 |
|
| 41 |
8 |
2.56578 |
|
| 42 |
9 |
2.58117 |
|
| 43 |
10 |
2.59374 |
|
| 44 |
1010 |
2.71694 |
|
| 45 |
2010 |
2.71761 |
|
| 46 |
3010 |
2.71783 |
|
| 47 |
4010 |
2.71794 |
|
| 48 |
5010 |
2.71801 |
|
| 49 |
6010 |
2.71806 |
|
| 50 |
7010 |
2.71809 |
|
| 51 |
8010 |
2.71811 |
|
| 52 |
9010 |
2.71813 |
|
| 53 |
10010 |
2.71815 |
|
| 54 |
11010 |
2.71816 |
|
| 55 |
12010 |
2.71817 |
|
| 56 |
very large |
|
<==Value of
"e" used by Excel |
|
| 57 |
1000 |
|
<=EXP(1) |
|
| 58 |
Natural
logarithms use "e" as their base. |
|
| 59 |
So the log to the base e
is the value you need to raise e to get the number |
|
| 60 |
|
| 61 |
Spreadsheets use a
special set of functions to manipulate the natural logs. |
|
| 62 |
|
| 63 |
To get the natural
logarithm use =ln(number) |
|
| 64 |
To get the anti-logarithm
(to reverse the process) use =exp(mumber) |
|
| 65 |
|
| 66 |
|
| 67 |
|
Number |
ln(number) |
|
Result |
|
| 68 |
|
1 |
0.000000 |
=
2.71828182845905 ^ 0 = |
|
1 |
|
| 69 |
|
2 |
0.693147 |
=
2.71828182845905 ^ 0.693147180559945 = |
2 |
|
| 70 |
|
5 |
1.609438 |
=
2.71828182845905 ^ 1.6094379124341 = |
5 |
|
| 71 |
|
7 |
1.945910 |
=
2.71828182845905 ^ 1.94591014905531 = |
7 |
|
| 72 |
|
10 |
2.302585 |
=
2.71828182845905 ^ 2.30258509299405 = |
10 |
|
| 73 |
|
25 |
3.218876 |
=
2.71828182845905 ^ 3.2188758248682 = |
25 |
|
| 74 |
|
|
|
| 75 |
So again
exp(ln(number)=number |
|
| 76 |
|
| 77 |
|
Number |
|
| 78 |
|
1000 |
1000 |
<=EXP(LN(C78)) |
|
| 79 |
|
| 80 |
|
| 81 |
|
| 82 |
|
| 83 |
|
|
|
|
|
|
|
|
|
|
|
|

